In my work on Internet use and religion, one of the recurring questions is whether the analysis I am doing, primarily regression models using observational data, provides evidence that Internet use causes decreased religiosity, or only shows a statistical association between them.
I discuss this question in the next section, which is probably too long. If you get bored, you can skip to the following section, which presents a different method for estimating effect size, a "propensity score matching estimator", and compares the results to the regression models.
What does "evidence" mean?
In the previous article I presented results from two regression models and made the following argument:
- Internet use predicts religiosity fairly strongly: the effect size is stronger than education, income, and use of other media (but not as strong as age).
- Controlling for the same variables, religiosity predicts Internet use only weakly: the effect is weaker than age, date of interview, income, education, and television (and about the same as radio and newspaper).
- This asymmetry suggests that Internet use causes a decrease in religiosity, and the reverse effect (religiosity discouraging Internet use) is weaker or zero.
- It is still possible that a third factor could cause both effects, but the control variables in the model, and asymmetry of the effect, makes it hard to come up with plausible ideas for what the third factor could be.
I am inclined to consider these results as evidence of causation (and not just a statistical association).
When I make arguments like this, I get pushback from statisticians who assert that the kind of observational data I am working with cannot provide any evidence for causation, ever. To understand this position better, I posted
this query on reddit.com/r/statistics. As always, I appreciate the thoughtful responses, even if I don't agree. The top-rated comments came from /u/Data_Driven_Dude, who states this position:
Causality is almost wholly a factor of methodology, not statistics. Which variables are manipulated, which are measured, when they're measured/manipulated, in what order, and over what period of time are all methodological considerations. Not to mention control/confounding variables.
So the most elaborate statistics in the world can't offer evidence of causation if, for example, a study used cross-sectional survey design. [...]
Long story short: causality is a helluva lot harder than most people believe it to be, and that difficulty isn't circumvented by mere regression.
I believe this is a consensus opinion among many statisticians and social scientists, but to be honest I find it puzzling. As I argued
in this previous article, correlation is in fact evidence of causation, because observing a correlation is more likely if there is causation than if there isn't.
The problem with correlation is not that it is powerless to demonstrate causation, but that a simple bivariate correlation between A and B can't distinguish between A causing B, B causing A, or a confounding variable, C, causing both A and B.
But regression models can. In theory, if you control for C, you can measure the causal effect of A on B. In practice, you can never know whether you have identified and effectively controlled for all confounding variables. Nevertheless, by adding control variables to a regression model, you can find evidence for causation. For example:
- If A (Internet use, in my example) actually causes B (decreased religiosity), but not the other way around, and we run regressions with B as a dependent variable, and A as an explanatory variable, we expect find that A predicts B, of course. But we also expect the observed effect to persist as we add control variables. The magnitude of the effect might get smaller, but if we can control effectively for all confounding variables, it should converge on the true causal effect size.
- On the other hand, if we run the regression the other way, using B to predict A, we expect to find that B predicts A, but as we add control variables, the effect should disappear, and if we control for all confounding variables, it should converge to zero.
For example,
in this previous article, I found that first babies are lighter than others, by about 3 ounces. However, the mothers of first babies tend to be younger, and babies of younger mothers tend to be lighter. When I control for mother's age, the apparent effect is smaller, less than an ounce, and no longer statistically significant. I conclude that mother's age explains the apparent difference between first babies and others, and that the causal effect of being a first baby is small or zero.
I don't think that conclusion is controversial, but here's the catch: if you accept "the effect disappears when I add control variables" as evidence against causation, then you should also accept "the effect persists despite effective control for confounding variables" as evidence for causation.
Of course the key word is "effective". If you think I have not actually controlled for an important confounding variable, you would be right to be skeptical of causation. If you think the controls are weak, you might accept the results as weak evidence of causation. But if you think the controls are effective, you should accept the results as strong evidence.
So I don't understand the claim that regression models cannot provide any evidence for causation, at all, ever, which I believe is the position my correspondents took, and which seems to be taken as a truism among at least some statisticians and social scientists.
I put this question to /u/Data_Driven_Dude, who wrote the following:
[...]just because you have statistical evidence for a hypothesized relationship doesn't mean you have methodological evidence for it. Methods and stats go hand in hand; the data you gather and analyze via statistics are reflections of the methods used to gather those data.
Say there is compelling evidence that A causes B. So I hypothesize that A causes B. I then conduct multiple, methodologically-rigorous studies over several years (probably over at least a decade). This effectively becomes my research program, hanging my hat on the idea that A causes B. I become an expert in A and B. After all that work, the studies support my hypothesis, and I then suggest that there is overwhelming evidence that A causes B.
Now take your point. There could be nascent (yet compelling) research from other scientists, as well logical "common sense," suggesting that A causes B. So I hypothesize that A causes B. I then administer a cross-sectional survey that includes A, B, and other variables that may play a role in that relationship. The data come back, and huzzah! Significant regression model after controlling for potentially spurious/confounding variables! Conclusion: A causes B.
Nope. In your particular study, ruling out alternative hypotheses by controlling for other variables and finding that B doesn't predict A when those other variables are considered is not evidence of causality. Instead, what you found is support for the possibility that you're on the right track to finding causality. You found that A tentatively predicts B when controlling for XYZ, within L population based on M sample across N time. Just because you started with a causal hypothesis doesn't mean you conducted a study that can yield data to support that hypothesis.
So when I say that non-experimental studies provide no evidence of causality, I mean that not enough methodological rigor has been used to suppose that your results are anything but a starting point. You're tiptoeing around causality, you're picking up traces of it, you see its shadow in the distance. But you're not seeing causality itself, you're seeing its influence on a relationship: a ripple far removed from the source.
I won't try to summarize or address this point-by-point, but a few observations:
- One point of disagreement seems to be the meaning of "evidence". I admit that I am using it in a Bayesian sense, but honestly, that's because I don't understand any alternatives. In particular, I don't understand the distinction between "statistical evidence" and "methodological evidence".
- Part of what my correspondent describes is a process of accumulating evidence, starting with initial findings that might not be compelling and ending (a decade later!) when the evidence is overwhelming. I mostly agree with this, but I think the process starts when the first study provides some evidence and continues as each additional study provides more. If the initial study provides no evidence at all, I don't know how this process gets off the ground. But maybe I am still stuck on the meaning of "evidence".
- A key feature of this position is the need for methodological rigor, which sounds good, but I am not sure what it means. Apparently regression models with observational data lack it. I suspect that randomized controlled trials have it. But I'm not sure what's in the middle. Or, to be more honest, I know what is considered to be in the middle, but I'm not sure I agree.
To pursue the third point, I am exploring methods commonly used in the social sciences to test causality.
SKIP TO HERE!
Matching estimators of causal effects
I'm reading Morgan and Winship's
Counterfactuals and Causal Inference, which is generally good, although it has the academic virtue of presenting simple ideas in complicated ways. So far I have implemented one of the methods in
Counterfactuals, a
propensity score matching estimator. Matching estimators work like this:
- To estimate the effect of a particular treatment, D, on a particular outcome, Y, we divide an observed sample into a treatment group that received D and a control group that didn't.
- For each member of the treatment group, we identify a member of the control group that is as similar as possible (I'll explain how soon), and compute the difference in Y between the matched pair.
- Averaging the observed differences over the pairs yields an estimate of the mean causal effect of D on Y.
The hard part of this process is matching. Ideally the matching process should take into account all factors that cause Y. If the pairs are identical in all of these factors, and differ only in D, any average difference in Y must be caused by D.
Of course, in practice we can't identify all factors that cause Y. And even if we could, we might not be able to observe them all. And even if we could, we might not be able to find a perfect match for each member of the treatment group.
We can't solve the first two problems, but "propensity scores" help with the third. The basic idea is
- Identify factors that predict D. In my example, D is Internet use.
- Build a model that uses those factors to predict the probability of D for each member of the sample; this probability is the propensity score. In my example, I use logistic regression with age, income, education, and other factors to compute propensity scores.
- Match each member of the treatment group with the member in the control group with the closest propensity score. In my example, the members of each pair have the same predicted probability of using the Internet (according to the model in step 2), so the only relevant difference between them is that one did and one didn't. Any difference in the outcome, religiosity, should reflect the causal effect of the treatment, Internet use.
I implemented this method (details below) and applied it to the data from the European Social Survey (ESS).
In each country I divide respondents into a treatment group with Internet use above the median and a control group below the median. We lose information by quantizing Internet use in this way, but the distribution tends to be bimodal, with many people at the extremes and few in the middle, so treating Internet use as a binary variable is not completely terrible.
To compute propensity scores, I use logistic regression to predict Internet use based on year of birth (including a quadratic term), year of interview, education and income (as in-country ranks), and use of other media (television, radio, and newspaper).
As expected, the average propensity in the treatment group is higher than in the control group. But some members of the control group are matched more often than others (and some not at all). After matching, the two groups have the same average propensity.
Finally, I compute the pair-wise difference in religiosity and the average across pairs.
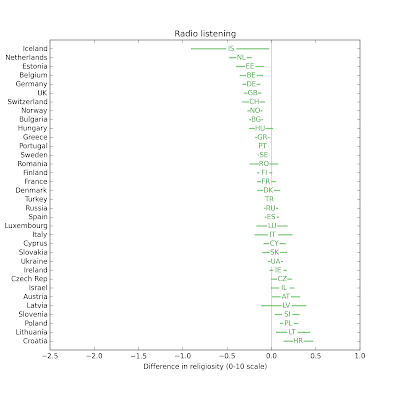
For each country, I repeat this process 101 times using weighted resampled data with randomly filled missing values. That way I can compute confidence intervals that reflect variation due to sampling and missing data. The following figure shows the estimated effect size for each country and a 95% confidence interval:
The estimated effect of Internet use on religiosity is negative in 30 out of 34 countries; in 18 of them it is statistically significant. In 4 countries the estimate is positive, but none of them are statistically significant.
The median effect size is 0.28 points on a 10 point scale. The distribution of effect size across countries is similar to the results from the regression model, which has median 0.33:
The confidence intervals for the matching estimator are bigger. Some part of this difference is because of the information we lose by quantizing Internet use. Some part is because we lose some samples during the matching process. And some part is due to the non-parametric nature of matching estimators, which make fewer assumptions about the structure of the effect.
How it works
The details of the method are in this IPython notebook, but I'll present the kernel of the algorithm here. In the following,
group is a Pandas DataFrame for one country, with one row for each respondent.
The first step is to quantize Internet use and define a binary variable,
treatment:
netuse = group.netuse_f
thresh = netuse.median()
if thresh < 1:
thresh = 1
group.treatment = (netuse >= thresh).astype(int)
The next step is use logistic regression to compute a propensity for each respondent:
formula = ('treatment ~ inwyr07_f + '
'yrbrn60_f + yrbrn60_f2 + '
'edurank_f + hincrank_f +'
'tvtot_f + rdtot_f + nwsptot_f')
model = smf.logit(formula, data=group)
results = model.fit(disp=False)
group.propensity = results.predict(group)
Next we divide into treatment and control groups:
treatment = group[group.treatment == 1]
control = group[group.treatment == 0]
And sort the controls by propensity:
series = control.propensity.sort_values()
Then do the matching by bisection search:
indices = series.searchsorted(treatment.propensity)
indices[indices < 0] = 0
indices[indices >= len(control)] = len(control)-1
And select the matches from the controls:
control_indices = series.index[indices]
matches = control.loc[control_indices]
Extract the distance in propensity between each pair, and the difference in religiosity:
distances = (treatment.propensity.values -
matches.propensity.values)
differences = (treatment.rlgdgr_f.values -
matches.rlgdgr_f.values)
Select only the pairs that are a close match
caliper = differences[abs(distances) < 0.001]
And compute the mean difference:
delta = np.mean(caliper)
That's all there is to it. There are better ways to do the matching, but I started with something simple and computationally efficient (it's n log n, where n is the size of the control or treatment group, whichever is larger).
Back to the philosophy
The agreement of the two methods provides some evidence of causation, because if the effect were spurious, I would expect different methodologies, which are more or less robust against the spurious effect, to yield different results.
But it is not very strong evidence, because the two methods are based on many of the same assumptions. In particular, the matching estimator is only as good as the propensity model, and in this case the propensity model includes the same factors as the regression model. If those factors effectively control for confounding variables, both methods should work. If they don't, neither will.
The propensity model uses logistic regression, so it is based on the usual assumptions about linearity and the distribution of errors. But the matching estimator is non-parametric, so it depends on fewer assumptions about the effect itself. It seems to me that being non-parametric is a potential advantage of matching estimators, but it doesn't help with the fundamental problem, which is that we don't know if we have effectively controlled for all confounding variables.
So I am left wondering why a matching estimator should be considered suitable for causal inference if a regression model is not. In practice one of them might do a better job than the other, but I don't see any difference, in principle, in their ability to provide evidence for causation: either both can, or neither.