This article is an excerpt from
Think Bayes, a book I am working on. The entire current draft is available from
http://thinkbayes.com. I welcome comments and suggestions.
The Price is Right Problem
On November 1, 2007, contestants named Letia and Nathaniel appeared
on
The Price is Right, an American game show. They competed in
a game called the Showcase, where the objective is to guess the price
of a showcase of prizes. The contestant who comes closest to the
actual price of the showcase, without going over, wins the prizes.
Nathaniel went first. His showcase included a dishwasher, a wine
cabinet, a laptop computer, and a car. He bid $26,000.
Letia’s showcase included a pinball machine, a video arcade game, a
pool table, and a cruise of the Bahamas. She bid $21,500.
The actual price of Nathaniel’s showcase was $25,347. His bid
was too high, so he lost.
The actual price of Letia’s showcase was $21,578. She was only
off by $78, so she won her showcase and, because
her bid was off by less than $250, she also won Nathaniel’s
showcase.
For a Bayesian thinker, this scenario suggests several questions:
- Before seeing the prizes, what prior beliefs should the
contestant have about the price of the showcase?
- After seeing the prizes, how should the contestant update
those prior beliefs?
- Based on the posterior distribution, what should the
contestant bid?
The third question demonstrates a common use of Bayesian analysis:
optimization. Given a posterior distribution, we can choose
the bid that maximizes the contestant’s expected return.
This problem is inspired by an example in Cameron Davidson-Pilon’s
book,
Bayesian Methods for Hackers.
The prior
To choose a prior distribution of prices, we can take advantage
of data from previous episodes. Fortunately, fans of the show
keep detailed records. When I corresponded with Mr. Davidson-Pilon
about his book, he sent me data collected by Steve Gee at
http://tpirsummaries.8m.com. It includes the price of
each showcase from the 2011 and 2012 seasons, and the bids
offered by the contestants.
| Figure 6.1: Distribution of prices for showcases on The Price is Right, 2011-12. |
Figure
6.1 shows the distribution of prices for these
showcases. The most common value for both showcases is around
$28,000, but the first showcase has a second mode near $50,000,
and the second showcase is occasionally worth more than $70,000.
These distributions are based on actual data, but they
have been smoothed by Gaussian kernel density estimation (KDE).
So before we go on, I want to take a detour to talk about
probability density functions and KDE.
Probability density functions
So far [in
Think Bayes, that is] we have been working with probability mass functions, or PMFs.
A PMF is a mapping from each possible value to its probability. In my
implementation, a
Pmf object provides a method named
Prob that
takes a value and returns a probability, also known as a “probability
mass.”
A probability density function, or PDF, is the continuous version of a
PMF, where the possible values make up a continuous range rather than
a discrete set.
In mathematical notation, PDFs are usually written as functions; for
example, here is the PDF of a Gaussian distribution with
mean 0 and standard deviation 1:
To represent this PDF in Python, I could define a class like this:
class StandardGaussianPdf(object):
def Density(self, x):
return math.exp(-x**2)
Density takes a value,
x, and returns the probability
density evaluated at
x.
A probability density is similar
to a probability mass in one way: higher density indicates that a
value is more likely.
But a density is not a probability. If you integrate a density
over a continuous range, the result is a probability. But
for the applications in this book we seldom have to do that.
In this book we primarily use probability densities as part
of a
Likelihood function. We will see an example soon.
Representing Pdfs
Before we get back to
The Price is Right, I want to
present a more general way to represent PDFs.
thinkbayes.py provides a class named
Pdf that defines
two functions,
Density and
MakePmf:
class Pdf(object):
def Density(self, x):
raise UnimplementedMethodException()
def MakePmf(self, xs):
pmf = Pmf()
for x in xs:
pmf.Set(x, self.Density(x))
pmf.Normalize()
return pmf
Pdf is an
abstract type, which means that it defines
the interface a Pdf is supposed to have, but does not provide
a complete implementation. Specifically,
Pdf provides
MakePmf but not
Density. [PMFs are described in
Chapter 2 of Think Bayes.]
A
concrete type is a class that extends an abstract parent
class and provides an implementation of the missing methods.
For example,
GaussianPdf extends
Pdf and provides
Density:
class GaussianPdf(Pdf):
def __init__(self, mu, sigma):
self.mu = mu
self.sigma = sigma
def Density(self, x):
density = scipy.stats.norm.pdf(x,
loc=self.mu,
scale=self.sigma)
return density
__init__ takes
mu and
sigma, which are
the mean and standard deviation of the distribution.
Density uses a function from
scipy to evaluate the
Gaussian PDF.
The Gaussian PDF is defined by a simple mathematical function,
so it is easy to evaluate. And it is useful because many
quantities in the real world have distributions that are
approximately Gaussian.
But with real data, there is no guarantee that the PDF
is Gaussian, or any other simple mathematical function. In
that case we can use a data sample to estimate the PDF of
the whole population.
For example, in
The Price Is Right data, we have
313 prices for the first showcase. We can think of these
values as a sample from the population of all possible showcase
prices.
Near the middle of the distribution, we see the following values:
| 28800, 28868, 28941, 28957, 28958 |
In the sample, no values appear between 28801 and 28867, but
there is no reason to think that these values are impossible.
Based on our background information, we would expect all
values in this range to be equally likely. In other words,
we expect the PDF to be reasonably smooth.
Kernel density estimation (KDE) is an algorithm that takes
a sample of values and finds an appropriately-smooth PDF that fits
the data. You can read about the details at
http://en.wikipedia.org/wiki/Kernel_density_estimation.
scipy provides an implementation of KDE.
thinkbayes
provides a class called
EstimatedPdf that extends
Pdf
and uses KDE:
class EstimatedPdf(Pdf):
def __init__(self, sample):
xs = numpy.array(sample, dtype=numpy.double)
self.kde = scipy.stats.gaussian_kde(xs)
def Density(self, x):
return self.kde.evaluate(x)
__init__ takes a sample, converts it to a NumPy array,
and computes a kernel density estimate. The result is a
gaussian_kde object that provides an
evaluate
method.
Density takes a value, calls
gaussian_kde.evaluate,
and returns the resulting density.
Finally, here’s an outline of the code I used to generate
Figure
6.1:
prices = ReadData()
kde = thinkbayes.EstimatedPdf(prices)
low, high = 0, 75000
n = 101
xs = numpy.linspace(low, high, n)
pmf = kde.MakePmf(xs)
myplot.Pmf(pmf)
And now back to
The Price is Right.
Modeling the contestants
The PDFs in Figure
6.1 estimate the
distribution of possible prices for each showcase.
If you were a contestant on the show, you could use this
distribution to quantify
your prior belief about the price of the showcases
(before you see the prizes).
To update these priors, you have to answer these questions:
- What data should we consider and how should we quantify it?
- Can we compute a Likelihood function; that is,
for each hypothetical value of price, can we compute
the conditional likelihood of the data?
To answer these questions, I am going to model the contestant
as a price-guessing instrument with known error characteristics.
In other words, when the contestant sees the prizes, he or she
guesses the price of each prize—ideally without taking into
consideration the fact that the prize is part of a showcase—and
adds up the prices. Let’s call this total
guess.
Under this model, the question we have to answer is, “If the
actual price is
price, what is the likelihood that the
contestant’s total estimate would be
guess?”
Or if we define
error = price - guess
then we could ask, “What is the likelihood
that the contestant’s estimate is off by
error?”
To answer this question, we can use the historical data again.
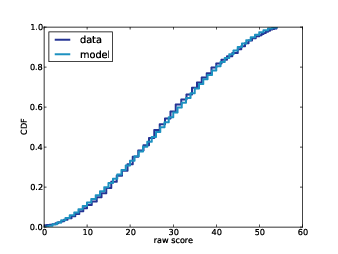
Figure
6.2 shows the cumulative distribution of
diff,
the difference between the contestant’s bid and the actual price
of the showcase.
The definition of diff is
diff = price - bid
When
diff is negative, the bid is too high. As an
aside, we can use this CDF to compute the probability that the
contestants overbid: the first contestant overbids 25% of the
time; the second contestant overbids 29% of the time.
| Figure 6.2: Cumulative distribution (CDF) of the difference between the contestant’s bid and the actual price. |
We can also use this distribution to estimate the reliability of
the contestants’ guesses. This step is a little tricky because
we don’t actually know the contestant’s guesses; we only know
what they bid.
In Figure
6.2 we can see that the bids are biased;
that is, they are more likely to be too low than too high. And
that makes sense, given the rules of the game.
So we’ll have to make some assumptions. Specifically, I assume
that the distribution of
error is Gaussian with mean 0
and the same variance as
diff.
The
Player class implements this model:
class Player(object):
def __init__(self, price, bid, diff):
self.price = price
self.bid = bid
self.diff = diff
self.pdf_price = thinkbayes.EstimatedPdf(price)
self.cdf_diff = thinkbayes.MakeCdfFromList(diff)
mu = 0
sigma = numpy.std(self.diff)
self.pdf_error = thinkbayes.GaussianPdf(mu, sigma)
price is a sequence of showcase prices,
bid is a
sequence of bids, and
diff is a sequence of diffs, where
again
diff = price - bid.
pdf_price is the smoothed PDF of prices, estimated by KDE.
cdf_diff is the cumulative distribution of
diff,
which we saw in Figure
6.2. And
pdf_error
is the PDF that characterizes the distribution of errors; where
error = price - guess.
Again, we use the variance of
diff to estimate the variance of
error. But contestant’s bids are sometimes strategic; for
example, if Player 2 thinks that Player 1 has overbid, Player 2 might
make a very low bid. In that case
diff does not reflect
error. If this strategy is common, the observed variance in
diff might overestimate the variance in
error. Nevertheless,
I think it is a reasonable modeling decision.
As an alternative, someone preparing to appear on the show could
estimate their own distribution of
error by watching previous shows
and recording their guesses and the actual prices.
Likelihood
Now we are ready to write the likelihood function. As usual,
I define a new class that extends
thinkbayes.Suite:
class Price(thinkbayes.Suite):
def __init__(self, pmf, player):
thinkbayes.Suite.__init__(self)
for price, prob in pmf.Items():
self.Set(price, prob)
self.player = player
pmf represents the prior distribution. The
for
loop copies the values and probabilities from
pmf into
the new
Suite.
player is a Player object as described in the previous
section. And here’s
Likelihood:
def Likelihood(self, hypo, data):
price = hypo
guess = data
error = price - guess
like = self.player.ErrorDensity(error)
return like
hypo is the hypothetical price of the showcase.
data
is the contestant’s best guess at the price.
error is
the difference, and
like is the likelihood of the data,
given the hypothesis.
ErrorDensity is defined in
Player:
# class Player:
def ErrorDensity(self, error):
return self.pdf_error.Density(error)
ErrorDensity works by evaluating
pdf_error at
the given value of
error.
The result is a probability density, which means we can’t treat it as
a probability. But remember that
Likelihood does not really
need to compute a probability; it only has to compute something
proportional to a probability. As long as the constant of
proportionality is the same for all likelihoods, it gets cancelled out
when we normalize the posterior distribution.
And therefore, a probability density is a perfectly good likelihood.
Update
Player provides a method that takes the contestant’s
guess and computes the posterior distribution:
def MakeBeliefs(self, guess):
pmf = self.PmfPrice()
self.prior = Price(pmf, self, name='prior')
self.posterior = self.prior.Copy(name='posterior')
self.posterior.Update(guess)
PmfPrice evaluates
pdf_price at an equally-spaced
series of values:
def PmfPrice(self):
return self.pdf_price.MakePmf(self.price_xs)
The result is a new
Pmf object, which we use to construct
the prior. To construct the posterior, we make a copy of the
prior and then invoke
Update, which invokes
Likelihood
for each hypothesis, multiplies the priors by the likelihoods,
and then renormalizes.
So let’s get back to the original scenario. Suppose you are
Player 1 and when you see your showcase, your best guess is
that the total price of the prizes is $20,000.
The following code constructs and plots your prior and
posterior beliefs about the actual price:
player1.MakeBeliefs(20000)
myplot.Pmf(player1.prior)
myplot.Pmf(player2.prior)
| Figure 6.3: Prior and posterior distributions for Player 1, based on a best guess of $20,000. |
Figure
6.3 shows the results. The value of your guess
is on the low end of the prior range, so the posterior is shifted
to the left. The mean of the posterior is $25,096; the most
likely value is $24,000.
On one level, this result makes sense. The most likely value
in the prior is $27,750. Your best guess is $20,000. And the
most likely value in the posterior is about half way in between.
On another level, you might find this result bizarre, because it
suggests that if you think the price is $20,000, then you
should believe the price is $24,000.
To resolve this apparent paradox, remember that you are combining two
sources of information, historical data about past showcases and
guesses about the prizes you see.
We are treating the historical data as the prior and updating it
based on your guesses, but we could equivalently use your guess
as a prior and update it based on historical data.
If you think of it that way, maybe it is less surprising that the
most likely value in the posterior is not your original guess.
In
the next installment, we'll use the posterior distribution to compute the optimal bid for each player.