Think Complexity

Think Complexity

On Friday I turned in the manuscript for Think Complexity, which will be published by O'Reilly Media in March (or, at least, that's the schedule). For people who can't stand to wait that long, I am going to publish excerpts here.  And if you really can't wait, you can read the free version at thinkcomplex.com.

The book is about data structures and algorithms, intermediate programming in Python, computational modeling and the philosophy of science:

• Data structures and algorithms: A data structure is a collection of data elements organized in a way that supports particular operations.  For example, a Python dictionary organizes key-value pairs in a way that provides fast mapping from keys to values, but mapping from values to keys is slower. An algorithm is a mechanical process for performing a computation. Designing efficient programs often involves the co-evolution of data structures and the algorithms that use them.  For example, in the first few chapters I present graphs, data structures that implement graphs, and graph algorithms based on those data structures.
• Python programming: Think Complexity picks up where Think Python leaves off.  I assume that you have read that book or have equivalent knowledge of Python.  I try to emphasize fundamental ideas that apply to programming in many languages, but along the way I present some useful features that are specific to Python.
• Computational modeling: A model is a simplified description of a system used for simulation or analysis. Computational models are designed to take advantage of cheap, fast computation.
• Philosophy of science: The experiments and results in this book raise questions relevant to the philosophy of science, including the nature of scientific laws, theory choice, realism and instrumentalism, holism and reductionism, and epistemology.

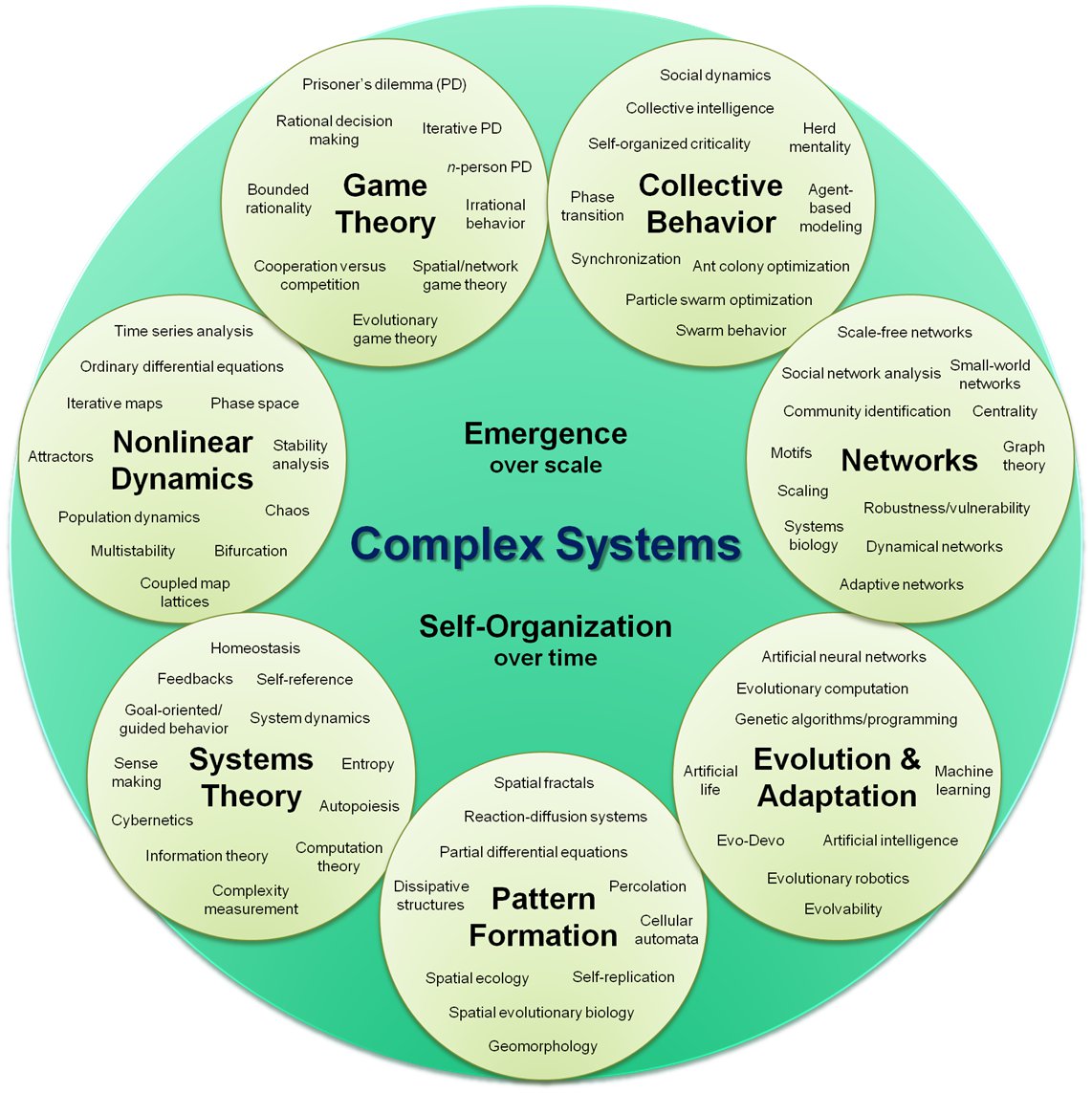
The book is also about complexity science, which is an interdisciplinary field---at the intersection of mathematics, computer science and natural science---that focuses on discrete models of physical systems.  In particular, it focuses on complex systems, which are systems with many interacting components.

Complex systems include networks and graphs, cellular automata, agent-based models and swarms, fractals and self-organizing systems, chaotic systems and cybernetic systems.  Here is a framework for these topics (from http://en.wikipedia.org/wiki/Complex_systems).

A new kind of science?

In 2002 Stephen Wolfram published A New Kind of Science where he presents his and others' work on cellular automata and describes a scientific approach to the study of computational systems.  There's a chapter about cellular automata in the book, but for now I'm going to borrow his title for something a little broader.

I think complexity is a ``new kind of science'' not because it applies the tools of science to a new subject, but because it uses different tools, allows different kinds of work, and ultimately changes what we mean by ``science.''

To demonstrate the difference, I'll start with an example of classical science: suppose someone asked you why planetary orbits are elliptical.  You might invoke Newton's law of universal gravitation and use it to write a differential equation that describes planetary motion.  Then you could solve the differential equation and show that the solution is an ellipse.  Voila!

Most people find this kind of explanation satisfying.  It includes a mathematical derivation---so it has some of the rigor of a proof---and it explains a specific observation, elliptical orbits, by appealing to a general principle, gravitation.

Let me contrast that with a different kind of explanation.  Suppose you move to a city like Detroit that is racially segregated, and you want to know why it's like that.  If you do some research, you might find a paper by Thomas Schelling called ``Dynamic Models of Segregation,'' which proposes a simple model of racial segregation (you can download the paper here).

Here is an outline of the paper's primary experiment:

• The Schelling model of the city is an array of cells where each cell represents a house.  The houses are occupied by two kinds of agents, labeled red and blue, in roughly equal numbers.  About 10% of the houses are empty.   
• At any point in time, an agent might be happy or unhappy, depending on the other agents in the neighborhood.  In one version of the model, agents are happy if they have at least two neighbors like themselves, and unhappy if they have one or zero.
• The simulation proceeds by choosing an agent at random and checking to see whether it is happy.  If so, nothing happens; if not, the agent chooses one of the unoccupied cells at random and moves.

If you start with a simulated city that is entirely unsegregated and run the model for a short time, clusters of similar agents appear.  As time passes, the clusters grow and coalesce until there are a small number of large clusters and most agents live in homogeneous neighborhoods.

The degree of segregation in the model is surprising, and it suggests an explanation of segregation in real cities.  Maybe Detroit is segregated because people prefer not to be greatly outnumbered and will move if the composition of their neighborhoods makes them unhappy.    

Is this explanation satisfying in the same way as the explanation of planetary motion?  Most people would say not, but why?

Most obviously, the Schelling model is highly abstract, which is to say not realistic.  It is tempting to say that people are more complex than planets, but when you think about it, planets are just as complex as people (especially the ones that have people).

Both systems are complex, and both models are based on simplifications; for example, in the model of planetary motion we include forces between the planet and its sun, and ignore interactions between planets.

The important difference is that, for planetary motion, we can defend the model by showing that the forces we ignore are smaller than the ones we include.  And we can extend the model to include other interactions and show that the effect is small.  For Schelling's model it is harder to justify the simplifications.

To make matters worse, Schelling's model doesn't appeal to any physical laws, and it uses only simple computation, not mathematical derivation.  Models like Schelling's don't look like classical science, and many people find them less compelling, at least at first. But as I will try to demonstrate, these models do useful work, including prediction, explanation, and design.  One of the goals of Think Complexity is to explain how.

In the next excerpt, I will present some of the ways I think complexity science differs from classical science.  But in the meantime I welcome comments on Part One.